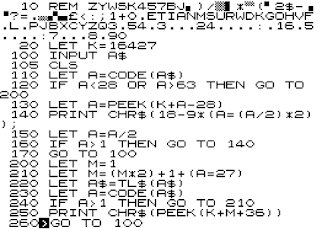
Mini-Morse is a type-in 1K ZX81 program, but it's also a little treatise on encoding and Morse tutorials. Firstly, the listing which you can type in using an on-line ZX81 Emulator. Type POKE 16389,68 <Newline> New <Newline> to reduce the ZX81's memory to a proper 1K and then continue with the listing.
The Tutor
Then you can type RUN <Newline> to start it. It's really simple to use, just type a letter or digit and it'll convert the character to a morse code made of dots and dashes. Alternatively, type a sequence of '.'s (to the right of the 'M') and '-'s (Shift+J), fairly quickly and it'll translate your Morse code. In that case it's best to select the sequence you want and remember it, then type it out rather than trying to read and copy it. You'll find you'll pick up the technique fairly quickly. It only shows one letter at a time.
This is always the kind of Morse Tutor I would have wanted to use, even though it doesn't care about the relative lengths of the dots and dashes. That's because I want a low-barrier to entry and I don't want it to be too guided, with me having to progress from Level 1 to whatever they've prescribed. Also, the basics of Morse code is simple, so a program that handles it should be simple.
Encoding
So, here's the interesting bit. What's the easiest way to encode Morse? Here's the basic international set from the Wikipedia Morse Code entry:
The Puzzle with Morse code is that it's obvious that it's a kind of binary encoding, but at the same time it can't quite be, because many of the patterns have equivalent binary values. For example E= '.' = 0 = I = '..' = S = '...' = H = '....' = 5 = '.....'. Every pattern <=5 symbols will have at least one other letter or number with an equivalent binary value.
When people type in Morse they solve the problem by generating a third symbol - a timing gap between one letter and the next. And in tables of Morse code the same thing is done, at least one extra symbol is added - usually an extended space at the end of the symbol.
This implies that Morse can be encoded the same way on a computer, by encoding it as a set of variable-length strings (which involves the use of a terminating symbol or a length character), or encoding it in base 3 (so that a third symbol can be represented).
However, we should feel uneasy about this as an ideal, because everything about Morse code itself, still looks like it's in binary. Shouldn't it be possible to encode it as such?
The Trick
The answer is yes! And here's the trick. The key thing to observe when trying to convert Morse into pure binary is that every symbol is equivalent to another with an indefinite number of 0s prepended. As in my examples above, both E and H would be 0 in an 8-bit encoding: 00000000 and 00000000. So, all we have to do to force them to be different is to prevent the most significant digit from being part of an indefinite number of 0s, by prepending a 1. This splits the indefinite preceding 0s from the morse encoding. Then E and H become: 00000010 and 00010000. Of course, when it comes to displaying the symbols we'd begin after the first 1 digit. Another way of looking at it is to observe that the length is encoded by the number of 0s preceding the first '1' or the number of digits following the first '1', but the true insight is to grasp that this works for a variable-length morse-type encoding up to any number of dots and dashes.
You can persuade yourself that this works by trying it out on a number of Morse symbols above. An implication of this technique is that it means we know we can encode Morse in 1+the maximum sequence length bits. Here we only use basic letters and numbers so we only need 6 bits at most.
In the program above, Morse code uses that trick to encode using a pair of strings. K$ converts digits and letters into dots and dashes while M$ converts dots and dashes into digits and letters. I could have used just one string and searched through it to find the other mapping, but this is faster.
One thing else to note. M$ encodes dots and dashes as you might expect (e.g. 'E' is at M$(2), because E is now '10'. However, K$ encodes characters into Morse in reverse bit order, because it's easier to test and strip the bottom bit from a value in ZX BASIC, which lacks bitwise operators. The same trick works regardless of the bit order: appending a '1' (or '-') at the end of all the patterns and then '.'s to a fixed length encodes unique patterns for all characters.
Conclusion
Learning Morse code is tedious. It was great for communications in the 19th century when the world had nothing better than the ability to create a momentary, electrical spark from making or breaking a contact on a single wire, but the symbols are all fairly random and hard to learn. This is not to understate the amazing tech breakthroughs they needed (e.g. amplifiers and water-proofing cables!).
I've wanted to write a simple Morse tutor for a while and a 1K ZX81 seems a natural platform for such a simple exercise. Plus, the Morse to character translation is a bit real-time and I really wanted to pass on the encoding trick. MiniMorse takes me full circle to a hack of mine in 2010 which created a morse-code type encoding for a POV display based on the layout of a phone keypad. Check out Hackaday's entry for PhorseCode or my Google Site web page for it. PhorseCode could be converted to a proper Morse Code system using a different translation table.
Postscript
It is, of course, possible to reduce the memory size of MiniMorse. Here's a version that's only a mere 405 bytes long, with just 32b of variables. I could reduce it a bit further by combining M and A as they're never used at the same time. Ironically, many of the space-saving techniques on the ZX81 make the program appear bigger. This is due to the fact that literal numbers incur a 6 byte overhead as the internal representation + prefix of CHR$ 114 gets inserted into the code. By employing tricks such as NOT PI for 0, SGN PI for 1, INT PI for 3; CODE "char" for any number in the range 2, 4 to 63 or 128 to 191; VAL "number" we can save bytes by preventing the internal representation from being used. Caching very frequently used values as variables can sometimes also save memory. Finally, the biggest difference was made by evaluating the K$ and M$ strings directly in the code, which saved over 128b because they're no longer duplicated in the variables region.
And there are yet more improvements. It's possible to replace a GOTO CODE [CHR$ 13] with GOTO PI; and string$<>"" with LEN string$; string$="" with NOT LEN string$; CODE [CHR$ 10] with PI*PI and finally we only need 4 spaces and no ';' on the print statement at the end. This takes it down to 393 bytes!
Mini-Morse ZX80
It's possible to write a variant of MiniMorse for the 1K ZX80. We need to do this in two parts. Strings can't be indexed on a ZX80; we can't type all the printable characters (can't type inverse characters); and some characters are remapped if you type them (e.g. PRINT CHR$(18), CODE("-") displays '-' then 220. You can find the character set near the end of the user manual at this URL.
So, instead we put the conversions in a REM statement and PEEK them. Programs start at 16424 and the first character of a REM statement is at 16427. So, the first stage is to enter all the Morse codes we can't easily enter (i.e. the letters).
RUN the program and type the values on the second row:
A.B. C. D E F. G. H. I J. K. L. M.N O. P. Q. R. S T U. V. W X. Y. Z
6 17 21 9 2 20 11 16 4 30 13 18 7 5 15 22 27 10 8 3 12 24 14 25 29 19
After it has run, check the REM statement matches the first line of the final program. When it does, delete lines 30 to 70 and complete the rest of the program as shown below:
MiniMorse for the ZX80 works slightly differently, because you have to press <Newline> after typing in the letter or Morse pattern you want to convert: the ZX80 doesn't support INKEY$. The easiest way to escape the program is by typing in 0 and then pressing <Space> immediately after pressing <Newline>.